理解 maps 的真正工作原理有可能相当困难，举个例子: 你是否曾经设置过 map 的 hint，即 make(map,hint)，为什么它叫 hint ，而不是slice那样的 len?

你可以已经注意到，当你在 map 上使用 for-range 时，顺序与插入顺序不匹配。如果在不同的时间循环同一个 map，每次的结果可能都不一样。奇怪的是，同一个时间循环，顺序通常保持不变。

跟上，带你看看。

本文基于 Go 1.23 版本。

快速开始

Go 中的 map，是一种内置类型，充当键值存储， key 可以是任何可比较的类型。

1
2
3
4
5

m := make(map[string]int)
m["a"] = 1
m["b"] = 2

m // map[a:1 b:2]

在该示例中，使用 make() 创建了一个空 map，其中 key 是字符串，value 是整数。

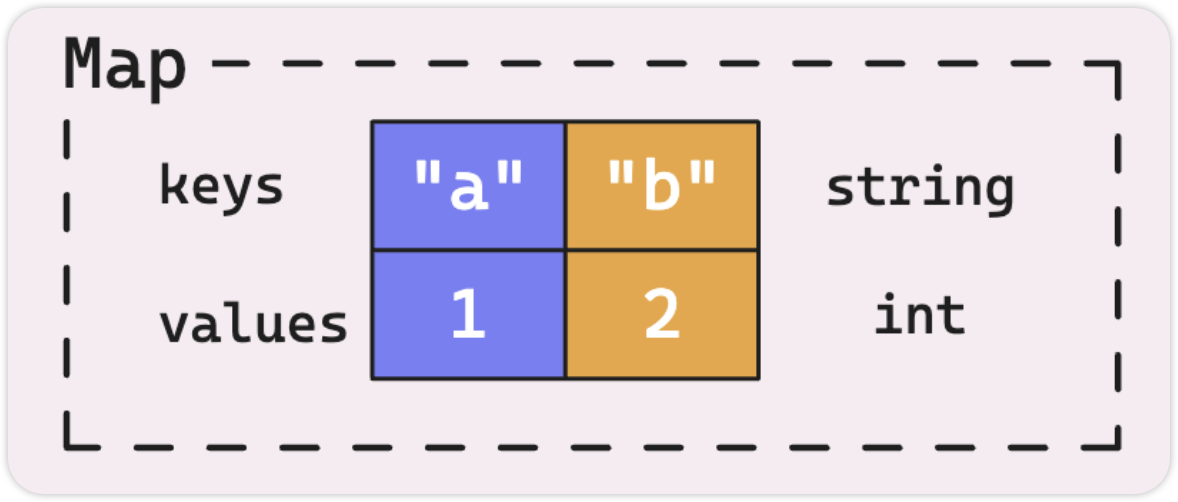
可以在声明 map 的同时赋值键值对。

1
2
3
4

m := map[string]int{
    "a": 1,
    "b": 2,
}

删除的方法是 delete(m,"a")

map 的零值是 nil，并且 nil map 在某些方面有点像 empty map，可以尝试在其中查找 key，golang 不会发生 panic 。

如果搜索不存在的 key，Go 会提供该类型的零值。

1
2
3
4

var m map[string]int

println(m["a"]) // 0
m["a"] = 1      // panic: assignment to entry in nil map

警告: 但不能对 nil map 添加新的键值对!

事实上， Go 处理 map 的方式与处理 slice 的方式非常相似，两者皆以 nil 开始，for-range 也不会发生 panic，Go 将任何类型的零值视为有用的东西，而不是导致程序崩溃的东西，除非当你做了一些非法的事情，例如尝试像 nil map 添加新的键值对，或者对 nil slice 越界索引。

关于 Go 中的 map，应该了解以下几点:

1. map 的遍历是乱序的
2. map 非线程安全，并且数据竞争时会发生 panic
3. 可以通过 ok 来检查 key 是否存在 _,ok := m[key]
4. map 的 key 必须是可比较的

那么，可比较类型到底是什么?

简单的很，如果可以使用 == 来判断相同类型的两个值，那么该类型被认为可以比较。

1
2
3
4
5
6
7
8
9

func main() {
    var s map[int]string

    if s == s {
        println("comparable")
    }
}

// compile error: invalid operation: s == s (map can only be compared to nil)

显然，上面的代码无法通过编译，map 只能与 nil 比较。

同样的规则适用于其他不可比较的类型，例如slice、函数或包含slice或map的结构等。

但这里有个小技巧，接口是可以比较的，也可以是不可比较的。

什么意思? 即可以定义一个空接口为键的 map ，而不会编译出错，但可以运行时出错。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12

func main() {
    m := map[interface{}]int{
        1: 1,
        "a": 2,
    }

    m[[]int{1, 2, 3}] = 3
    m[func() {}] = 4
}

// panic: runtime error: hash of unhashable type []int
// panic: runtime error: hash of unhashable type func()

一切看起来都很好，直到尝试分配一个不可比较的类型作为 key 。这比编译错误更难处理，应当避免使用 interface{} 作为 map 的 key 。

Map 剖析

让我们由浅入深，细品，别陷入 Go 源码的具体实现。

实际上，键值对是一个抽象，底层是由许多称为 bucket 的较小单元阻塞。

1
2
3
4
5

type hmap struct {
  ...
  buckets unsafe.Pointer
  ...
}

注意看，这个 buckets 是指针，这就是为什么将 map 分配给变量或传递给函数时，在外部的修改也会影响到这个值。

1
2
3
4
5
6
7
8
9

func changeMap(m2 map[string]int) {
  m2["hello"] = 2
}

func main() {
  m1 := map[string]int{"hello": 1}
  changeMap(m1)
  println(m1["hello"]) // 2
}

map 是指向运行时 hmap 的指针，但它们不是引用类型，如果如下所示的更改，它不会反映到调用者中。

1
2
3
4
5
6
7
8
9

func changeMap(m2 map[string]int) {
  m2 = map[string]int{"hello": 2}
}

func main() {
  m1 := map[string]int{"hello": 1}
  changeMap(m1)
  println(m1["hello"]) // 1
}

在 Go 中，一切都是按值传递的。真正发生的情况有点不同，当你将 map m1 传递给 changeMap 函数时，Go 会创建 *hmap 结构的副本。因此，main() 中的 m1 和 changeMap() 函数中的 m2 从技术上讲是指向相同 hmap 不同的指针。

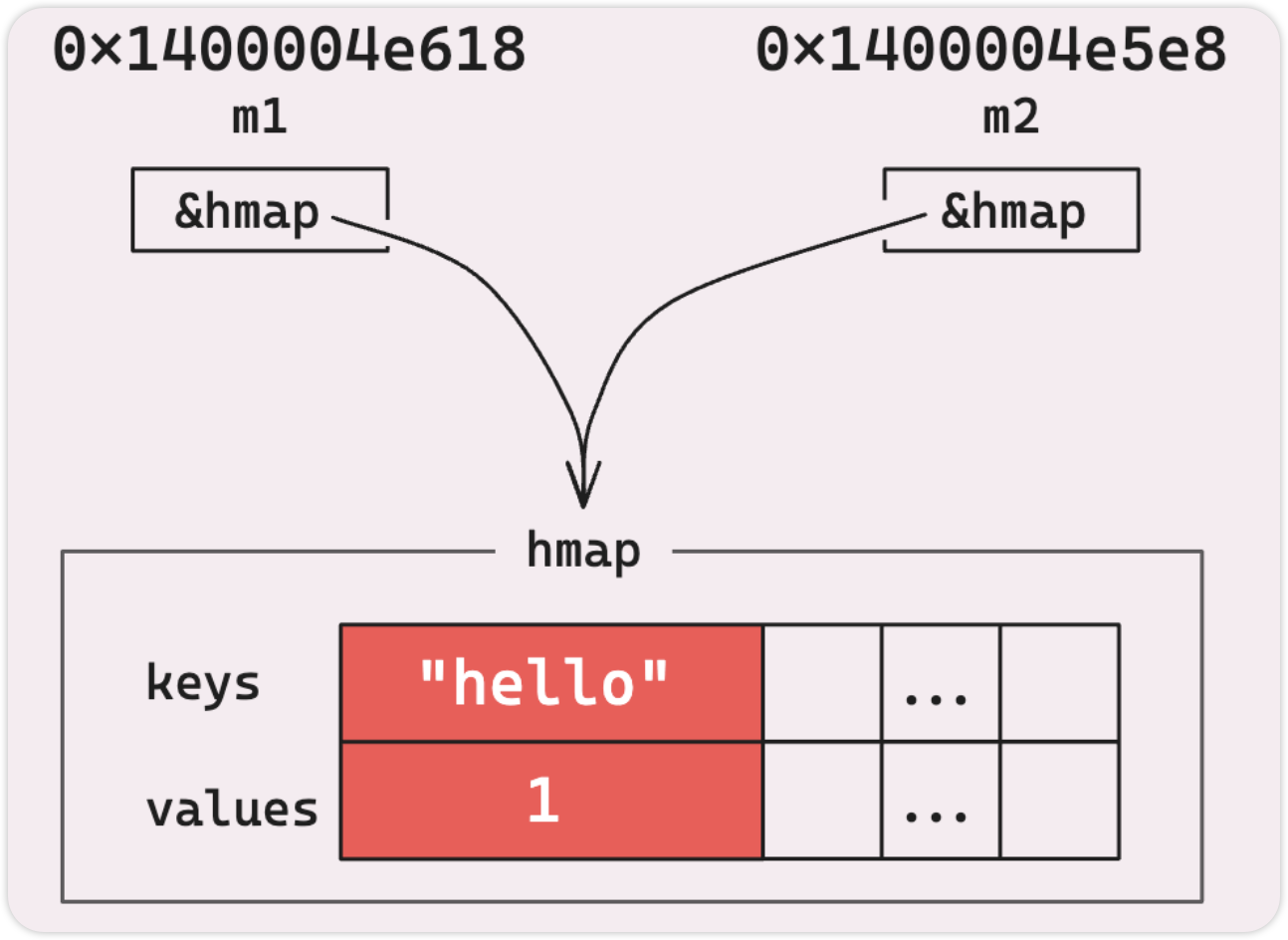
每个存储桶最多只能容纳 8 个键值对，如下图所示。

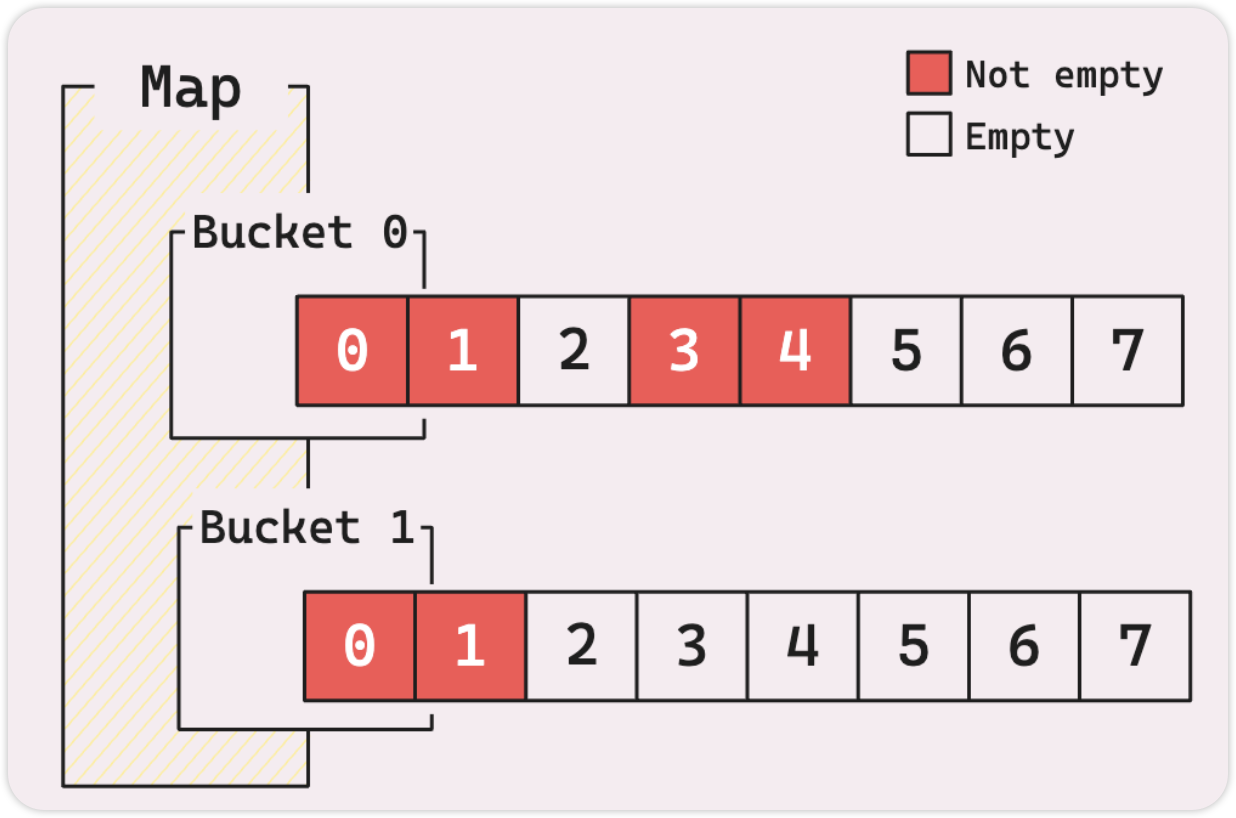
上面的map有2个bucket， len(map)是6。

当添加键值对时，会根据 hash(key, seed) 将键值对放入其中一个存储桶中。

看看以下场景: 有一个 nil map 并为其分配键值对

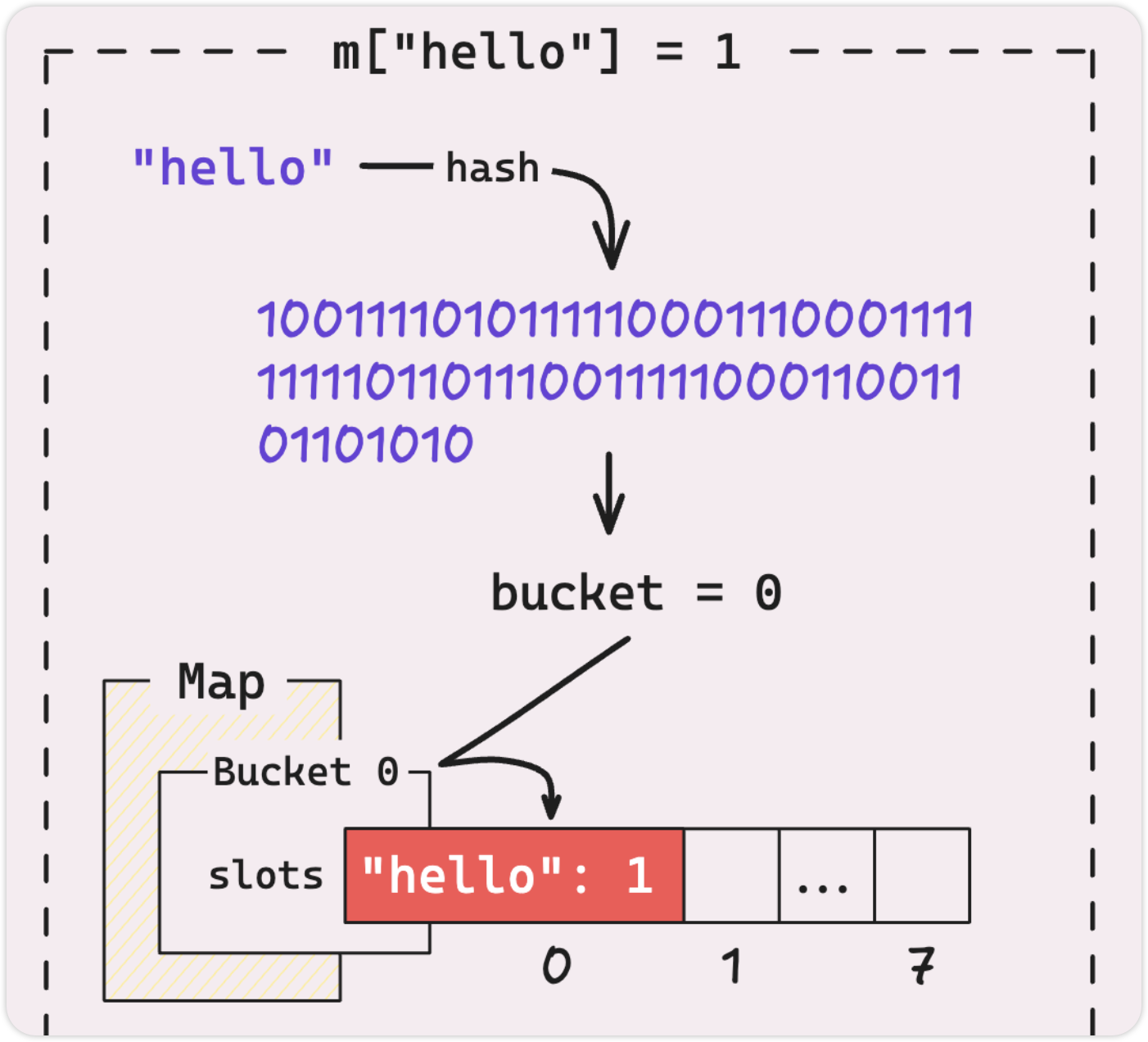
它首先将“hello”散列到一个数字，然后获取该数字并按存储桶的数量对其进行修改。

由于我们这里只有一个存储桶，任何数字 mod 1 都是 0，所以它会直接进入存储桶 0，当您添加另一个键值对时，也会发生相同的过程。它将尝试将其放入存储桶 0 中，如果第一个 bucket 已被占用或具有不同的密钥，它将移动到该存储桶中的下一个 bucket。

看一下hash(key, seed) ，当您在具有相同键的两个map上使用 for-range 循环时，您可能会注意到键以不同的顺序出现：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17

func main() {
	a := map[string]int{"a": 1, "b": 2, "c": 3, "d": 4, "e": 5, "f": 6}
	b := map[string]int{"a": 1, "b": 2, "c": 3, "d": 4, "e": 5, "f": 6}

	for i := range a {
		print(i, " ")
	}
	println()

	for i := range b {
		print(i, " ")
	}
}

// Output:
// a b c d e f
// c d e f a b

这怎么可能？map a 中的键“a”和map b 中的键“a”不是以相同的方式散列吗？

但事情是这样的，虽然 Go 中用于 map 的哈希函数在具有相同键类型的所有 map 中是一致的，但该哈希函数使用的seed对于每个 map 实例是不同的。因此，当您创建新 map 时，Go 会专门为该 map 生成一个随机种子。

一个 bucket 的长度最大是 8，那满了会怎样?

当桶开始变满，甚至几乎满时，根据算法对“满”的定义，map 将触发扩容，这可能会使 main buckets 的数量增加一倍。

有趣。

当我说“ main buckets” 时，我正在设置另一个概念：“overflow buckets”。当遇到高碰撞的情况时，这些就会发挥作用。试想: 存在 4 个bucket，但其中一个由于高冲突而完全装满，另外 3 个则空着。

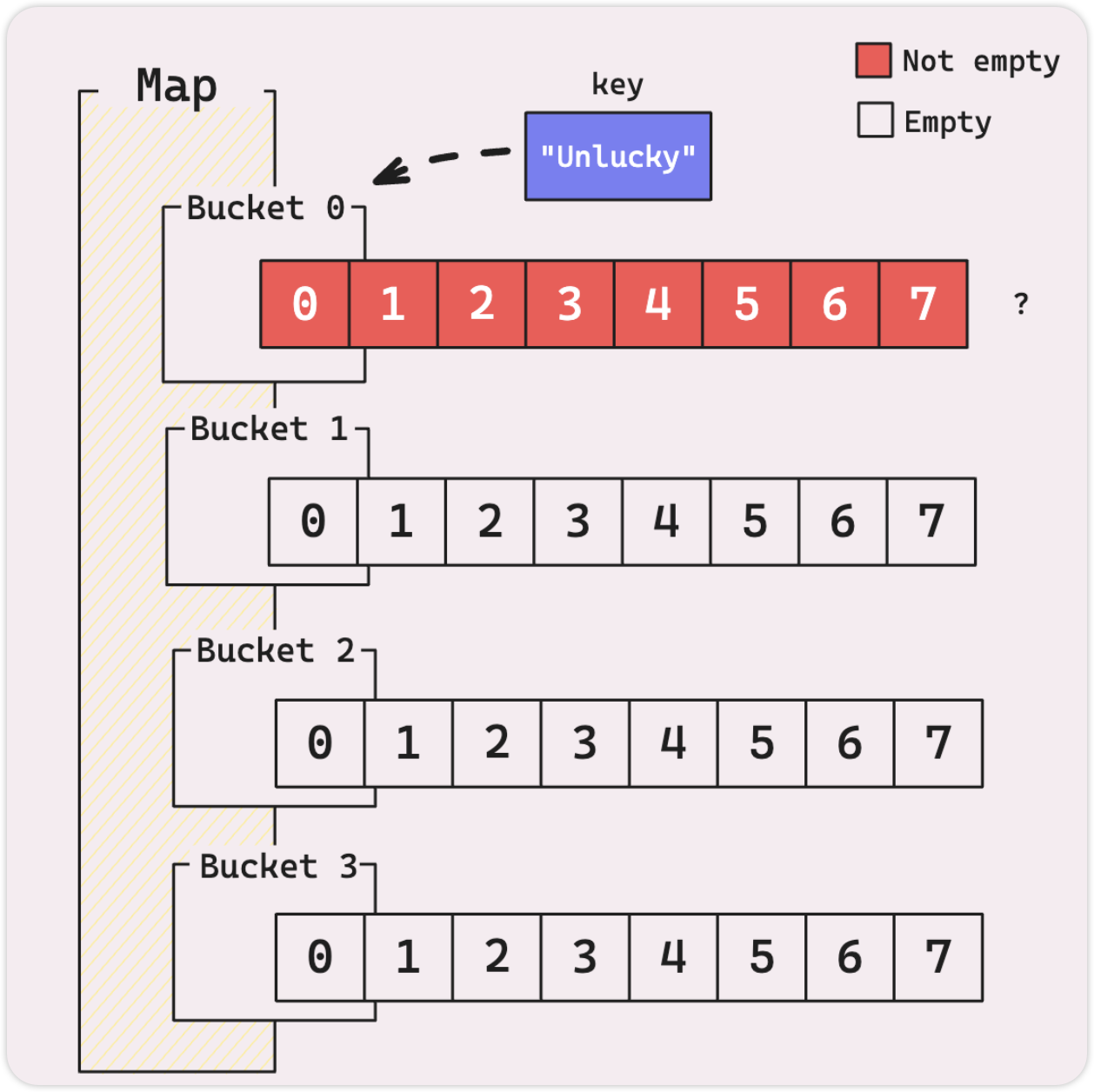
是否真的需要将 map 翻倍扩容到 8 个 buckets? 仅仅是需要添加一个不幸也落到 bucket 0 的键值对?

No! 这样太浪费了。

Go 通过创建链接到第一个 bucket 的 overflow bucket 来更有效处理这个问题。新的键值对存储在这个溢出桶中，而不是强制完全扩容。

当满足两个条件之一时，Go 中的 map 就会扩容: 要么溢出桶太多，要么 map 过载(负载因子太高)。

对应这两种条件，也有两种扩容方式:

• 翻倍扩容(过载时)
• 保持相同大小，但重新分配 bucket 中的数据。(当溢出桶太多时)

目前，Go 的负载因子设置为 6.5，这意味着 map 设计为每个 bucket 平均维护 6,5 个，大约是 80%的容量，当负载因子超过此阈值，map 视为过载。此时，将通过分配一个新的 buckets 数组，该数组是大小是当前的两倍，然后元素重新散列到新的 buckets 中。

我们通常认为在map中访问和赋值是 O(1)，对吧？但事情并不总是那么简单。

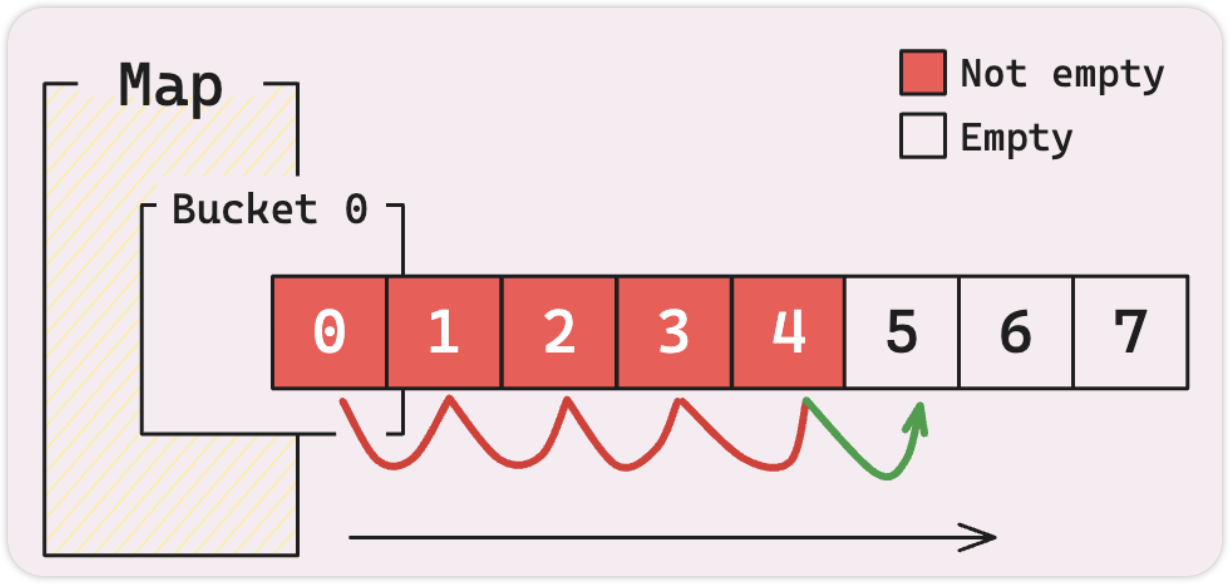
bucket 中的元素越多，速度就越慢。

当您想要添加另一个键值对时，不仅仅是检查存储桶是否有空间，而是将键与该存储桶中的每个现有键进行比较，以决定是添加新条目还是更新现有条目。

当您有溢出桶时，情况会变得更糟，因为您还必须检查这些溢出桶中的每个插槽。这种速度减慢也会影响访问和删除操作。

但 Go 团队强呀，他们为我们优化了这个比较。

还记得我们对键“Hello”进行散列时得到的散列吗？ Go 不只是把它扔掉。它实际上将“Hello”的 tophash 作为uint8缓存在存储桶中，并使用它与任何新密钥的 tophash 进行快速比较。这使得初始检查超级快。

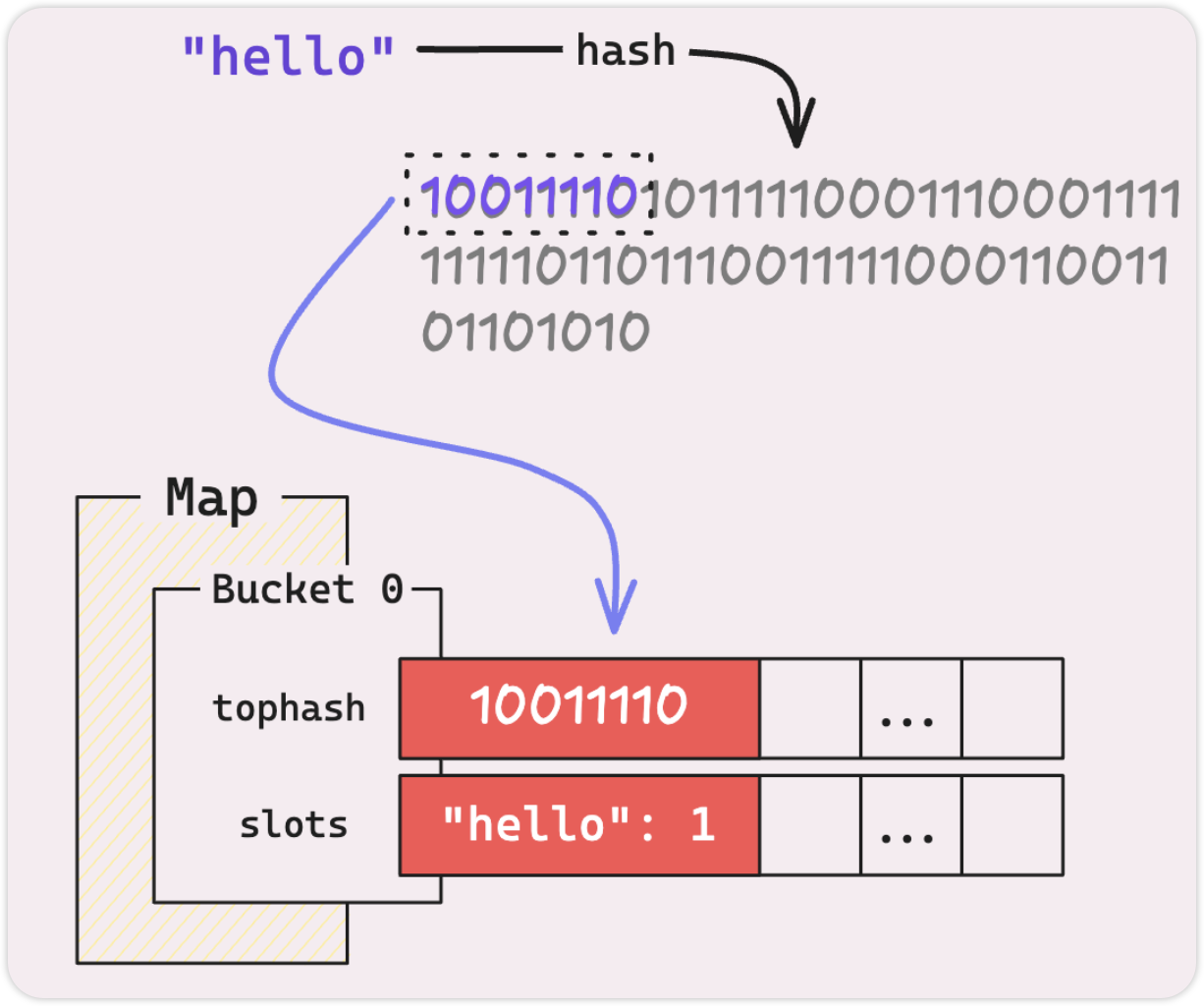
比较tophash后，如果它们匹配，则意味着密钥“可能”相同。然后，Go 继续进行较慢的过程，检查密钥是否实际上相同。

为什么使用 make(map,hint) 创建新 map 不提供确切的大小而只提供 hint？

make(map, hint)中的hint参数告诉Go您期望map保存的元素的初始数量。此 hint 有助于最大限度地减少添加元素时 map 需要扩容的次数。

由于每个扩容操作都涉及分配新的存储桶数组并复制现有元素，因此这不是最有效的过程。从较大的初始容量开始可以帮助避免一些成本高昂的扩容操作。

当您添加更多元素时，存储桶大小这样扩容：

为什么 hint= 14 会产生 4 个桶？我们只需要 2 个桶就可以容纳 14 个元素。

这就是负载因子发挥作用的地方，当 hint=13，有 2 个 buckets，负载因子为 13/2=6.5，达到阈值但未超过。因此，当 hint=14，负载因子超过 6.5，触发翻倍扩容。

hint=26也是如此，26/4=6.5，当 hint>26，map 需要扩容以有效容纳更多元素。

散列

为什么无法获取 map 元素的地址? 为什么不同时间不能保证范围内的顺序?

当 map 增长时，会分配一个新的 buckets 数组，是旧 buckets 的两倍，旧 buckets 中所有元素都变得无效，需要移动到新内存地址的 buckets 中。

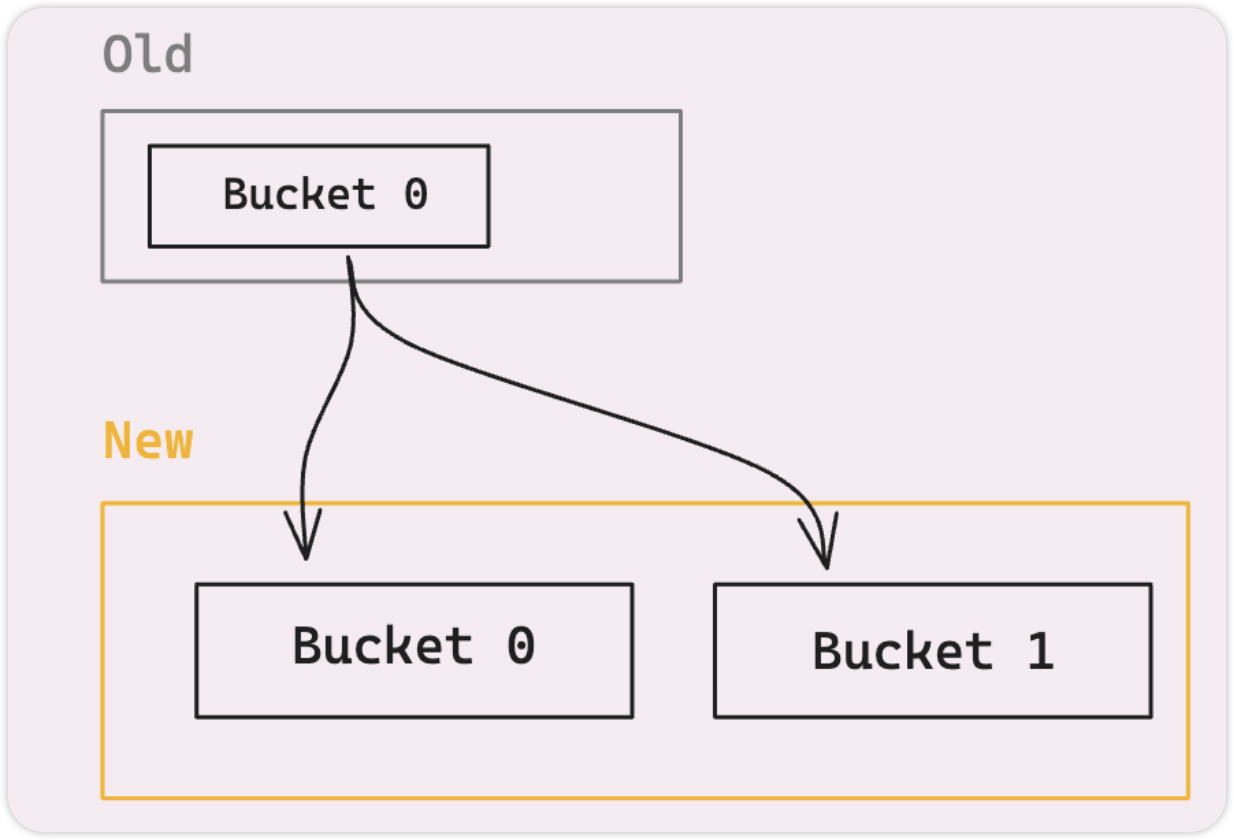
如果 map 很大，一次性的移动想当昂贵，可能在相当长的时间内阻塞 goroutine。为了避免这种情况，Go 使用增量的方式，一次只重新哈希一部分元素。你的程序可以保持平稳运行，不会突然出现滞后。

从旧 buckets 迁移到 新 buckets 什么时候发生?

两种情况:

• 添加新的键值对
• 从 map 中删除键值对

例如 map["hello"]=2 时，实际第一件事是清空包含 hello 的旧 buckets。

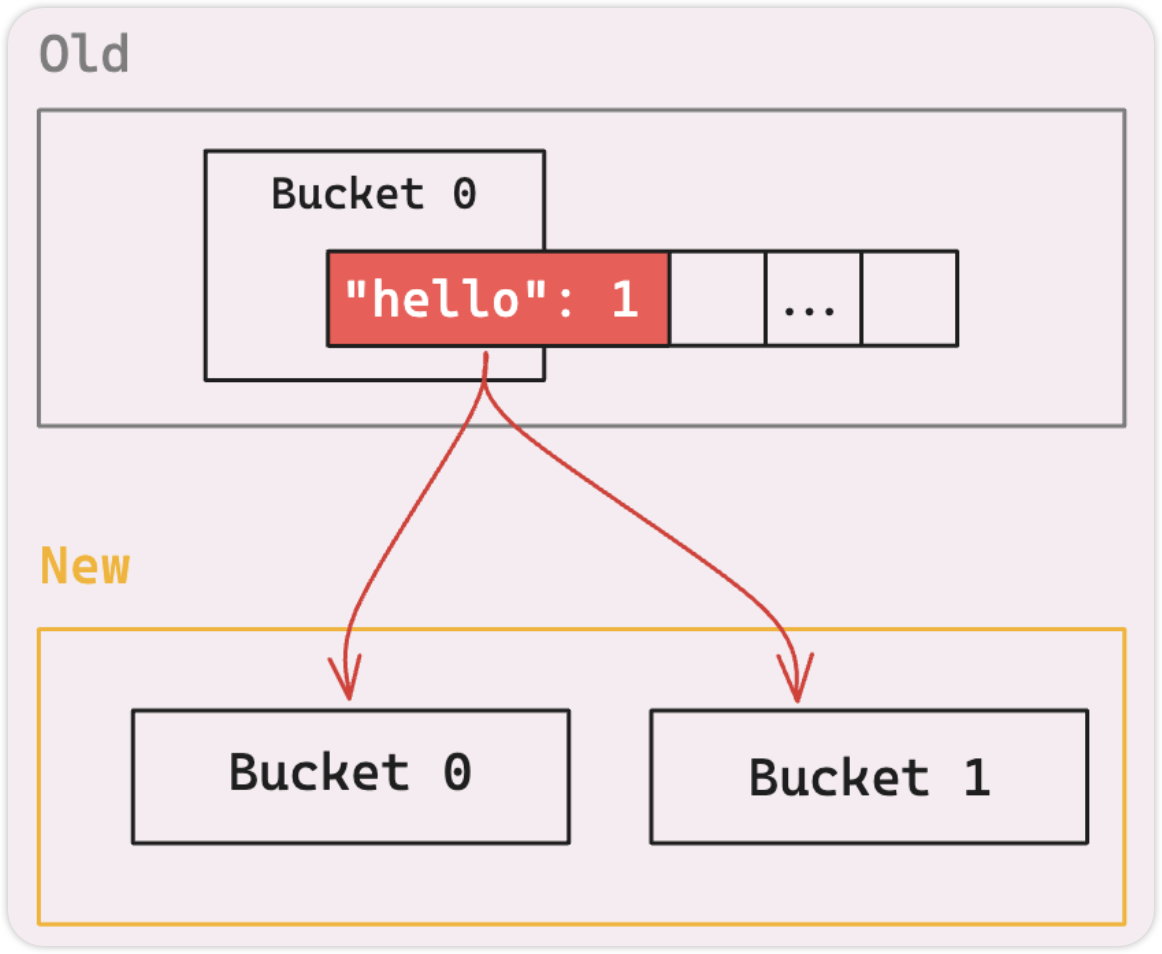
如果旧 buckets 有溢出桶， map 也会将这些 overflow buckets 的元素移动到新 buckets，移动所有元素后， map 通过在 tophash 字段将旧桶标记为 evacuated 。

先这么多哈，Go map 确实比这更复杂，很多小细节先不细说。

参考

本文翻译于 Go Maps Explained: How Key-Value Pairs Are Actually Stored